Written by: Amisha Shukla and Omer Shlomovits
Introduction:
Imagine a board filled with encrypted messages printed all over. There are ‘n’ recipients who are identified by public keys (pk). Imagine you are one of the recipients and now, you have to find out which message belongs to you. This entire process will take a very long time as in the worst case you have to scan every single message to find your message.
Note that the sender sends your auxiliary information as well along with the message, which will help you to identify your message on the board. It’s just like traditional letters wherein your name, address and contact details are written on the letter; anyone who gets that letter will know your name, address and contact details.
Here, this same information called ‘auxiliary information’ is like a signal which signals you got a message! So, if your friends went to collect their messages they will know that there is a message for you and they may signal you by saying, “Hey, there’s a message for you!”
The problem in the above scenario is that everyone knows that you have a new message. It’s like showcasing your emails publicly. This may seem like no big deal as only the subject of the email is visible, but a lot of information about your personal and professional life will be available for everyone. This is a serious hindrance to your privacy.
The question is how can the sender craft auxiliary information(signal) such that by looking at the signal and the board, no one, except you, can detect your message with no prior communication between you(recipient) and the sender?
Here, we are trying to protect even the fact that users received messages from a specific sender which is also known as relationship anonymity. The relationship anonymity is essential because even a single clue regarding data will lead to a higher probability of information leakage.
There must be a way with which we can actually take into account, both the anonymity of the message as well as the speed with which all the recipients can find their message.
We will compute a signal that allows only the intended recipient (and no one else) to learn that it’s the recipient of the posted message. Besides privacy, we also have some crucial efficiency requirements. First, the sender and recipient do not participate in any out-of-band communication, and second, the overhead of the recipient should be better than scanning the entire board.
That’s where private signaling comes in. Let’s dive in and learn the specific ways of making the entire process feasible, executable, quick, and secure.
We have two protocols – one with a single untrusted server (equipped with a trusted execution environment) and one with two untrusted (though not colluding) servers.
Some contributions on private signaling problems:
1. Formalization of the Private Signaling Problem:
Previous definitions were very informal and the security guarantees weren’t there. So, we have come up with a more formalized definition to help others understand the problem and contribute to it.
Private Signaling requires considering two properties: correctness and privacy
Correctness: guarantees that a recipient learns all the messages intended to them.
Privacy: Only the recipient can learn the location of its messages on the board
2. Protocols for private signaling with constant recipient overhead and provable UC- security:
In the following ideal case, the ‘server’ storing the locations of messages that are on the board, is trusted. The signal is simply the encryption of the location of the messages. Our goal is to maintain the privacy of the signals. Here is the flowchart showcasing the ideal protocol.
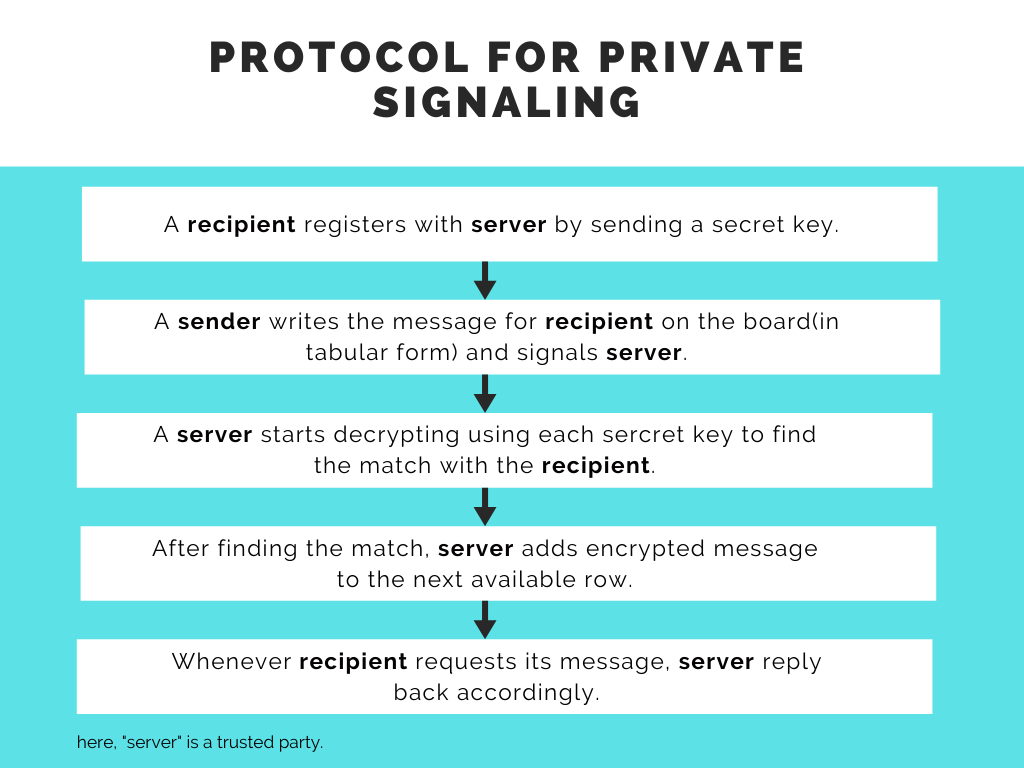
Now that we are familiar with the working of the protocol which achieves ‘correctness’; we have to achieve ‘privacy’. Our goal is to replace the trusted server with an untrusted sub-system that will achieve the same properties. The server must blindly decrypt and encrypt the messages without knowing the recipient.
We came up with two solutions:
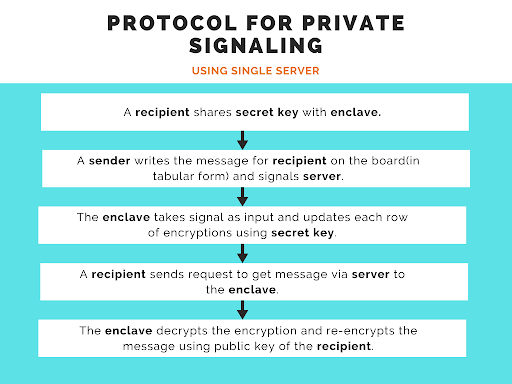
Solution 1: using single server
Here, a trusted execution environment (TEE) is used. The TEE is sort of a black box, running computations as defined, with no way to modify that or access the TEE state by the outside world.
A client can register with the TEE enclave within the server and is guaranteed that all computations inside the enclave are hidden to the server.
Here’s the flow chart of the process:
Solution 2: using two servers
Let us assume a public table of signals. Call this table T. Each line in the table corresponds to a recipient (R). To accomplish the goal of obliviously updating T, we can use two servers: Server₁ and Server₂ and have the table secret-shared among them.
Next, servers Server₁, Server₂ will update their tables by running a secure computation protocol.
Here is a concrete simple example of sending an encrypted message to Recipient number 3(R₃).
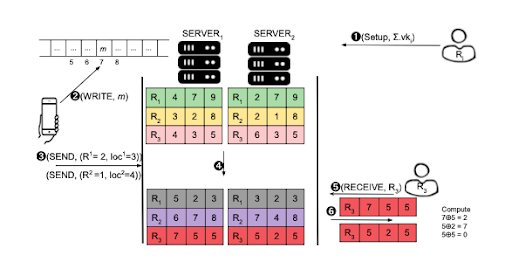
The protocol will follow these steps:
- Each recipient Rᵢ registers with the two servers.
- Sender writes message m for recipient R₃ on position 7 of the board.
- Sender creates shares of the row (recipient index) 3 = (2,1) such that 2⊕1 = 3 and the column number 7 = (3,4) such that 3⊕4 = 7 and send (2,3) to Server₁ and (1,4) to Server₂.
- Server₁ and Server₂ run a two party computation (2PC) with inputs (T₁, 2, 3) and (T₂, 1, 4) and some fresh randomness and output new tables T₁ and T₂ such that in the next available position of R₃’s row (column 2), update with shares of 7 = (5 and 2) (as 5 ⊕ 2 = 7) and re-randomize all other indices while maintaining the invariant that T1 [i][j ] ⊕ T2 [i][j ] remains the same.
- R₃ sends an authenticated request for its rows from the two servers.
- Server₁ sends [7,5,5] and Server₂ sends [5,2,5]. The recipient recombines the corresponding indices [7 ⊕ 5, 5 ⊕ 2, 5 ⊕ 5] = [2, 7, 0] to compute the locations of its messages.
The function being computed performs the following three elementary operations:
(1) Reconstruct recipient(R) and location(loc) by xoring the shares.
(2) Update the R-th row of the table to add loc to the first available index.
(3) Re-randomize every other row.
At the end of the secure computation of this function, each server receives a fresh share of the updated table, thus leaking no information about which row and column were actually updated.
Note that each recipient receives a different number of signals over time. To guarantee that no information about the number of messages per recipient is leaked, we introduce a parameter L. Each row in the table is of length L and each index is updated in the table per signal.
3. Open-source Implementations:
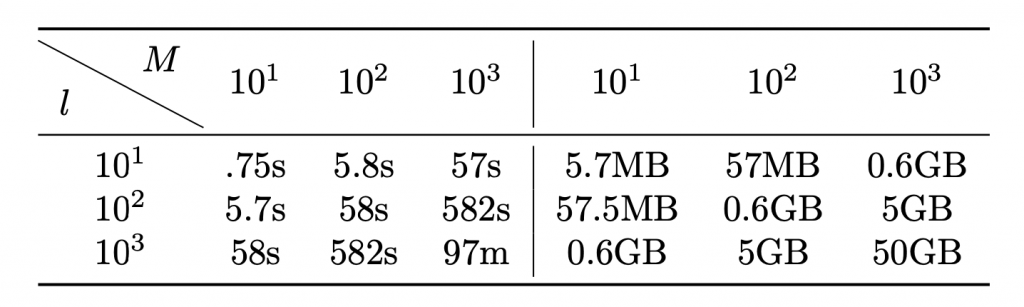
The performance is evaluated as a function of the number of recipients (M) and the upper bound of signals (L) received in each window of time by implementing both our protocols. The major advantage of our protocols is that they achieve the highest possible degree of anonymity.
Our protocols provide constant communication and computation complexity for the recipient and the sender. Specifically, a recipient only needs to perform a computation that is proportional to the number of signals it receives. Moreover, a sender only needs to compute constant size messages (either encryption or two shares of a location) and send them to the server(s). However, even in a naive setting, where one does not care about the privacy of the recipients, a server would need to do up to O(M) (in the worst case) computation to determine the recipient of the encrypted signal. Likewise, in both of our protocols, the overhead of the server(s) is O(LM) (where L is the number of signals a recipient can receive).
Depending on the application, one can choose different values for the parameters M and L. In our experiments we vary both M and L from 10 to 1000. From our implementation, we observe that we can trade off one parameter for the other to get a feasible efficiency for the server(s) (approx. 1 minute to process 100 signals for 100 recipients). We also observe that the single-server solution is more efficient than the two-server, but at the cost of a trusted setup (TEEs).
We also improve the efficiency of the 2-server protocol by having the servers process multiple signals at once.
Applications of Private Signaling:
Private signaling is a powerful abstraction since many real-world applications can be seen as a special case of it. We highlight two prominent and timely problems that can be cast as private signaling problems and consequently solved with our proposed solutions.
1. Stealth addresses and payments
Stealth addresses are very useful for making secure public transactions. In cryptocurrencies such as Ethereum, it is common to use static, public identities or addresses. However, sending recurring payments (e.g., salaries, donations, other regular purchases) to a static address that is publicly linked to an entity is harmful to both sender and recipient anonymity. To avert this issue, senders can generate so- called stealth addresses for their recipients. More specifically, given a recipient’s public address, the sender can non-interactively generate new “stealth” addresses for the intended recipient that are unlinkable to the recipient’s static, public address. Stealth addresses can only be redeemed by the true recipients. However, the difficulty is that recipients lack an efficient way to detect which stealth address belongs to them and are redeemable by them. Current implementations of stealth address payment systems apply the simple linear scan of the board as described earlier. Private signaling can be seen as a solution to alleviate the computation complexity of the recipient. More specifically, with private signaling, a sender first creates a transaction with a stealth address of recipient R and posts it to the board. Once the transaction is confirmed and the location of the transaction is known on the board, the sender sends a private signal to the server, who obliviously stores it. Now a recipient only needs to ask the server for its list of signals so it can identify its stealth address transactions directly.
2. Anonymous messaging
Modern private messaging applications are mostly focused on providing and improving sender anonymity, e.g., Signal’s sealed sender functionality. In anonymous messaging applications, senders post their messages to one (or more) untrusted store-and-forward server(s) or to a shared public bulletin board, as in Riposte, where the servers need to maintain the board. You can read more about anonymous messaging and privacy here.
Private signaling easily captures this problem in the following way: A sender first posts encrypted messages on a board. The sender then sends the locations of these messages to the server in a privacy-preserving way, such that only the recipient can retrieve the locations from the servers at a later point in time. Once the recipient has these locations it can simply decrypt the corresponding messages from the board to get their messages. Thus anonymous messaging can be seen as a special case of private signaling. Moreover, using our techniques, it is guaranteed that a recipient can retrieve its messages quickly and one can have arbitrary-sized messages that can be stored on the public board.
Conclusion and Open Problems:
Through this guide, we introduce the problem of private signaling that abstracts and generalizes several real-world recipient-anonymous applications. We have provided a formal definition in the UC framework, two server-aided protocols, and open-source implementations. The protocols achieve the best efficiency for the sender and recipients, requiring only minimal overhead.
To know more about ‘Private Signaling’, you can read the eprint version of the research paper.
The workload of the servers however is proportional to O(ML) per signal, which limits the choice of the parameters of M and L. We leave it as future work to explore techniques such as ORAM to improve the workload of the servers.
We release the source code of our implementations of private signaling protocols to facilitate further improvements and experiments. It can be found at https://github.com/Zengo-X/pps-gc.
